How to calculate the variance of a bet’a portfolio ?

Remember that a portfolio is a set of assets’The standard deviation of an asset that has three returns, i.e. 10, 12 and 14%, is an example of a financial instrument that can be made up of three different types of assets’I am careful not to put too many disparate assets such as bonds, futures, stocks and more in my portfolio. Investors manage portfolios in order to diversify and, consequently, to make money’avoid putting all their eggs in one basket, as the saying goes. In theory, if the’one of the investments generates losses, the other investments in a well diversified portfolio will not. The variance measures how the values of a stock are distributed’All of these assets are scattered with respect to the average, and its square root is the average’standard deviation of the mean.

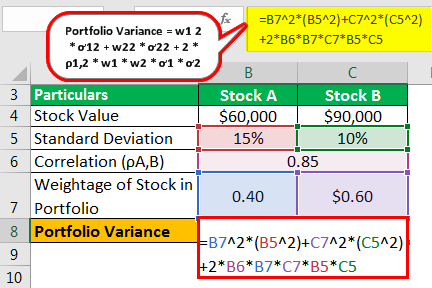
The variance of’a portfolio is made up of the variance of the assets that make it up, taking into account their respective weightings.

Calculate the weight and variance of each asset’Calculate the weight and variance of each asset

The weighting is the percentage that corresponds to each asset in the portfolio. L’How to calculate the variance of money in my betting account’The active bet can be calculated as the sum of all deviations from the average squared, divided by the number of values in the calculation. Let's take the’example of’an asset that has three returns: 10, 12 and 14%. The average is 12 and the number of values is three.

Thus, its variance will be ((10-12)^2+(12-12)^2+(12-12)^2+(14-12)^2)/3, or about 2.67.

Calculate the covariance of the two assets

Covariance is used to measure the degree of variation in the portfolio’unison of the two assets. It can be calculated as the sum of all deviations from the mean for both sets of values multiplied by the number of values. For example, the performance of two assets is recorded for three years. The former has yields of 10, 12 and 14%, while the latter has yields of 2, 8 and 14%. The average for the first asset is 12 and the average for the second asset is eight.

Thus, the covariance between the two would equal ((10-12)(2-8)+(12-12)(8-8)+(14-12)(14-8))/3, or eight.

Replace the numbers in the formula for calculating the portfolio differences to calculate them.

The portfolio variance is equal to the weight of the first asset squared by its variance plus the weight of the second asset squared by its variance plus twice its weights multiplied by its covariance. Using the’example above, assume that the weights of the two assets are 45 and 55%, their variances are 2.67 and 24, and their covariance is eight. By replacing these numbers in the formula, the portfolio variance would be equal to with a result of 11.76.

Advice

It is possible to calculate portfolio spreads for more than two assets by adjusting the formula. For example, the formula for calculating d’a portfolio of three assets is equal to the weight of the first asset squared multiplied by its variance, plus the weight of the second asset squared multiplied by its variance, plus the weight of the third asset squared multiplied by its variance, plus twice the weights of the first two assets multiplied by their covariance coefficient, plus twice the weights of the first and third assets multiplied by their covariance coefficient, plus twice the weights of the last two assets multiplied by their covariance coefficient.